文火|冰糖_[机器学习与scikitlearn19]：算法逻辑回归概述与原理

篇首语：本文由编程笔记#小编为大家整理，主要介绍了[机器学习与scikit-learn-19]：算法-逻辑回归-概述与原理相关的知识，希望对你有一定的参考价值。

作者主页(文火冰糖的硅基工坊)&＃xff1a;文火冰糖&＃xff08;王文兵&＃xff09;的博客_文火冰糖的硅基工坊_CSDN博客

本文网址&＃xff1a;https://blog.csdn.net/HiWangWenBing/article/details/123438808

目录

第1章 逻辑回归的应用场景

第2章 逻辑回顾在机器学习中的位置

第3章 逻辑回归与线性回归区分

第4章 什么逻辑回归

4.1 概述

4.2 链接函数与Sigmod

第5章 逻辑回顾的数学表达

第6章 sigmod函数的本质是概率吗

第7章 为什么需要逻辑回归&＃xff1a;逻辑回归的优势

第8本章 逻辑回归分类

8.1 线性回归

8.2 非线性回归

第1章 逻辑回归的应用场景

在银行借贷场景中&＃xff0c;评分卡是一种以分数形式来衡量一个客户的信用风险大小的手段&＃xff0c;它衡量向别人借钱的人&＃xff08;受信人&＃xff0c;需要融资的公司&＃xff09;不能如期履行合同中的还本付息责任&＃xff0c;并让借钱给别人的人&＃xff08;授信人&＃xff0c;银行等金融机构&＃xff09;造成经济损失的可能性。

一般来说&＃xff0c;评分卡打出的分数越高&＃xff0c;客户的信用越好&＃xff0c;风险越小。

这些”借钱的人“&＃xff0c;可能是个人&＃xff0c;有可能是有需求的公司和企业。对于企业来说&＃xff0c;我们按照融资主体的融资用途&＃xff0c;分别使用企业融资模型&＃xff0c;现金流融资模型&＃xff0c;项目融资模型等模型。而对于个人来说&＃xff0c;我们有”四张卡“来评判个人的信用程度&＃xff1a;A卡&＃xff0c;B卡&＃xff0c;C卡和F卡。

而众人常说的“评分卡”其实是指A卡&＃xff0c;又称为申请者评级模型&＃xff0c;主要应用于相关融资类业务中新用户的主体评级&＃xff0c;即判断金融机构是否应该借钱给一个新用户&＃xff0c;如果这个人的风险太高&＃xff0c;我们可以拒绝贷款。

备注&＃xff1a;

打分是连续的&＃xff0c;这个过程是线性拟合、线性回归。

根据打分后的信用评分&＃xff0c;先通过线性拟合的手段获得分数&＃xff0c;再根据分数进行分类&＃xff0c;打分和分类在同一个模型中一次性完成&＃xff0c;这就是逻辑回归。

“逻辑” &＃61;》 分类

“回归” &＃61;》 拟合

第2章 逻辑回顾在机器学习中的位置

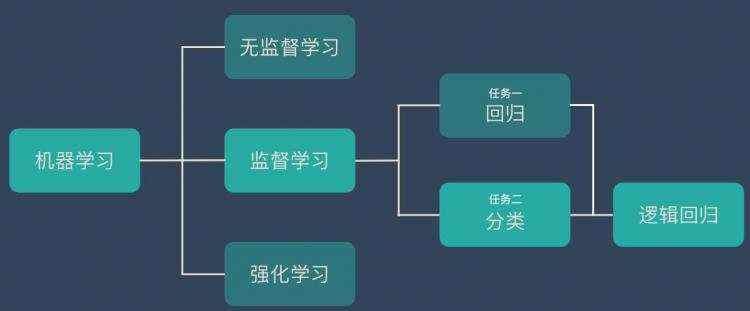
逻辑回归的目标是分类

逻辑回归的手段是回归

第3章 逻辑回归与线性回归区分

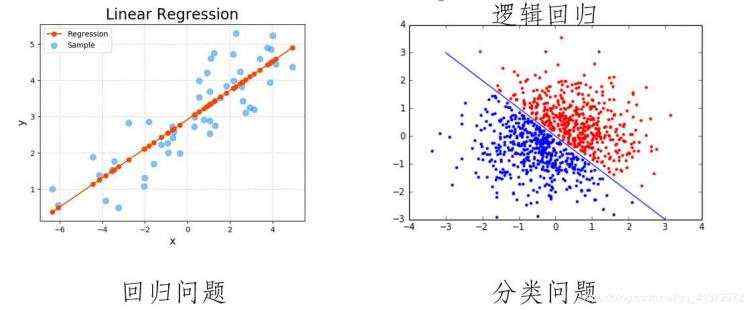
线性拟合回归&＃xff1a;用线性的曲线去拟合样本内在的走势。

线性逻辑回归&＃xff1a;用线性的曲线去分割样本的类别。

第4章 什么逻辑回归

4.1 概述

逻辑回归&＃xff0c;是一种名为“回归”的线性分类器&＃xff0c;其本质是由线性回归变化而来的&＃xff0c;一种广泛使用于分类问题中的广义回归算法。

要理解逻辑回归从何而来&＃xff0c;得要先理解线性回归。

线性回归是机器学习中最简单的的回归算法&＃xff0c;它写作一个几乎人人熟悉的方程&＃xff1a;

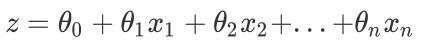
线性回归的任务&＃xff0c;就是构造一个预测函数 来映射输入的特征矩阵x和标签值y的线性关系&＃xff0c;而构造预测函数的核心就是找出模型的参数&＃xff1a;&＃xff0c;著名的最小二乘法就是用来求解线性回归中参数的数学方法。

通过函数 &＃xff0c;线性回归使用输入的特征矩阵X来输出一组连续型的标签值y_pred&＃xff0c;以完成各种预测连续型变量的任务&＃xff08;比如预测产品销量&＃xff0c;预测股价等等&＃xff09;。

那如果我们的标签是离散型变量&＃xff0c;尤其是&＃xff0c;如果是满足0-1分布的离散型变量&＃xff0c;我们要怎么办呢&＃xff1f;

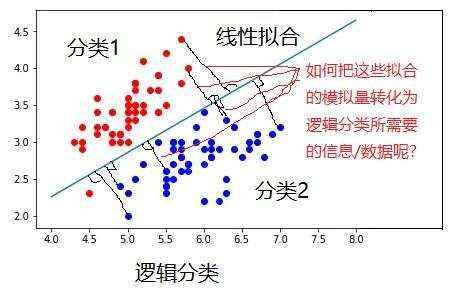
4.2 链接函数与Sigmod

我们可以通过引入链接函数(link function)&＃xff0c;将线性回归方程z变换为g(z)&＃xff0c;并且令g(z)的值分布在(0,1)之间&＃xff0c;且当g(z)接近0时样本的标签为类别0&＃xff0c;当g(z)接近1时样本的标签为类别1&＃xff0c;这样就得到了一个分类模型。

逻辑回归的本质是用函数拟合拟合的手段解决分类问题&＃xff0c;这在深度学习中得到了极大的体现。

深度学习就是利用大量的线性神经元来拟合复杂的现实世界&＃xff0c;并结合非线性的激活函数&＃xff0c;把他们组合在一起共同完成分类和拟合。

因此&＃xff0c;把回归转换为分类问题的过程中&＃xff0c;链接函数起着及其关键的作用。

而这个链接函数对于逻辑回归来说&＃xff0c;就是Sigmoid函数&＃xff1a;

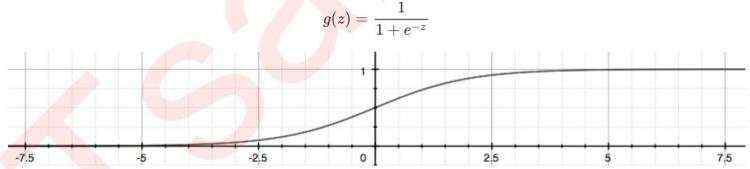
Sigmoid函数是一个S型的函数&＃xff1a;

当自变量z趋近正无穷时&＃xff0c;因变量g(z)趋近于1&＃xff0c;而当z趋近负无穷时&＃xff0c;g(z)趋近于0&＃xff0c;它能够将任何实数映射到(0,1)区间&＃xff0c;使其可用于将任意值函数转换为更适合二分类的函数。

因为这个性质&＃xff0c;Sigmoid函数也被当作是归一化的一种方法&＃xff0c;与我们之前学过的MinMaxSclaer同理&＃xff0c;是属于数据预处理中的“缩放”功能&＃xff0c;可以将数据压缩到[0,1]之内。区别在于&＃xff0c;MinMaxScaler归一化之后&＃xff0c;是可以取到0和1的&＃xff08;最大值归一化后就是1&＃xff0c;最小值归一化后就是0&＃xff09;&＃xff0c;但Sigmoid函数只是无限趋近于0和1。

Sigmoid函数在逻辑回归和打分中的重要意义&＃xff1a;

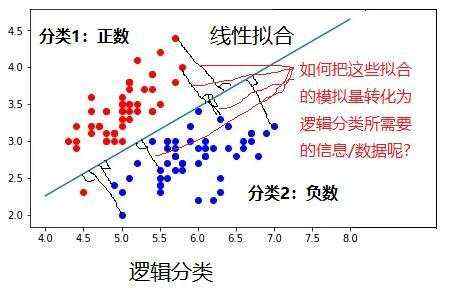
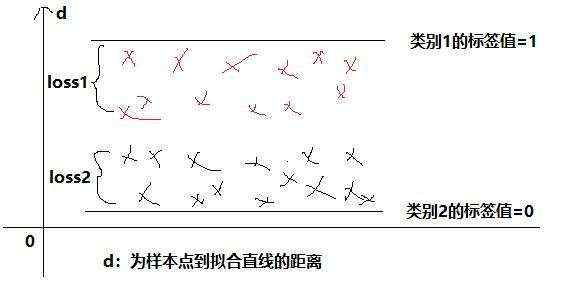
&＃xff08;1&＃xff09;把分类1对应的线性拟合出来的所有正数距离值值转换为[0.5, 1) 区间&＃xff0c;转为为所谓的[0.5, 1) 的概率值。这样分类化&＃xff0c;分类1的标签就是1.

&＃xff08;2&＃xff09;把分类1对应的线性拟合出来的所有正数距离值值转换为[0, 0.5) 区间&＃xff0c;转为为所谓的(0, 0.5] 的概率值。这样分类化&＃xff0c;分类2的标签就是0.

&＃xff08;3&＃xff09;转换后&＃xff0c;就是要找到一个线性直线&＃xff0c;使得标签1中所有点到直线的距离d1到分类1的标签值&＃xff1a;“1”的距离之和&＃xff0c;再加上标签2中所有点到直线的距离d2到分类2的标签值&＃xff1a;0的距离之和的loss值最小。如下图示意&＃xff1a;

第5章 逻辑回顾的数学表达

不难发现&＃xff0c;y(x)的形似几率取对数的本质其实就是我们的线性回归z&＃xff0c;我们实际上是在对线性回归模型的预测结果取对数几率来让其的结果无限逼近0和1。因此&＃xff0c;其对应的模型被称为”对数几率回归“&＃xff08;logistic Regression&＃xff09;&＃xff0c;也就是我们的逻辑回归&＃xff0c;这个名为“回归”却是用来做分类工作的分类器。之前我们提到过&＃xff0c;线性回归的核心任务是通过求解 构建 这个预测函数&＃xff0c;并希望预测函数 能够尽量拟合数据&＃xff0c;因此逻辑回归的核心任务也是类似的&＃xff1a;求解 来构建一个能够尽量拟合数据的预测函数 &＃xff0c;并通过向预测函数中输入特征矩阵来获取相应的标签值y。

第6章 sigmod函数的本质是概率吗

经过sigmod函数转换后&＃xff0c;距离d被转换成了[0,1] 之间的数值&＃xff0c;当给定一个样本&＃xff0c;算出其到拟合曲线的距离自然就是[0,1]之间&＃xff0c;转换后的特性与概率的特性及其相似&＃xff0c;这样就可以利用现成的概率相关的函数用来进行数学计算&＃xff0c;因此&＃xff0c;大多时候&＃xff0c;直接借用概率的概率来阐述了。

但本质上&＃xff0c;并非是真正意义上的概率&＃xff01;&＃xff01;&＃xff01;&＃xff01;这一点需要清醒的认知。

第7章 为什么需要逻辑回归&＃xff1a;逻辑回归的优势

有了用于拟合的回归&＃xff0c;有了专门用于分类的模型&＃xff0c;为啥还需要逻辑回归这一种模型呢?

它相对于普通的分类&＃xff08;如决策树分类&＃xff09;&＃xff0c;有什么优势与特点呢&＃xff1f;

线性回归&＃xff1a;对数据的要求很严格&＃xff0c;比如标签必须满足正态分布&＃xff0c;特征之间的多重共线性需要消除等等&＃xff0c;而现实中很多真实情景的数据无法满足这些要求&＃xff0c;因此线性回归在很多现实情境的应用效果有限。逻辑回归是由线性回归变化而来&＃xff0c;因此它对数据也有一些要求&＃xff0c;而我们之前已经学过了强大的分类模型决策树和随机森林&＃xff0c;它们的分类效力很强&＃xff0c;并且不需要对数据做任何预处理。
何况&＃xff0c;逻辑回归的原理其实并不简单。一个人要理解逻辑回归&＃xff0c;必须要有一定的数学基础&＃xff0c;必须理解损失函数&＃xff0c;正则化&＃xff0c;梯度下降&＃xff0c;海森矩阵等等这些复杂的概念&＃xff0c;才能够对逻辑回归进行调优。其涉及到的数学理念&＃xff0c;不比支持向量机少多少。况且&＃xff0c;要计算概率&＃xff0c;朴素贝叶斯可以计算出真正意义上的概率&＃xff0c;要进行分类&＃xff0c;机器学习中能够完成二分类功能的模型简直多如牛毛。因此&＃xff0c;在数据挖掘&＃xff0c;人工智能所涉及到的医疗&＃xff0c;教育&＃xff0c;人脸识别&＃xff0c;语音识别这些领域&＃xff0c;逻辑回归没有太多的出场机会。甚至&＃xff0c;在我们的各种机器学习经典书目中&＃xff0c;周志华的《机器学习》400页仅有一页纸是关于逻辑回归的&＃xff08;还是一页数学公式&＃xff09;&＃xff0c;《数据挖掘导论》和《Python数据科学手册》中完全没有逻辑回归相关的内容&＃xff0c;sklearn中对比各种分类器的效应也不带逻辑回归玩&＃xff0c;可见业界地位。

但是&＃xff0c;无论机器学习领域如何折腾&＃xff0c;逻辑回归依然是一个受工业商业热爱&＃xff0c;使用广泛的模型&＃xff0c;因为它有着不可替代的优点&＃xff1a;

&＃xff08;1&＃xff09;逻辑回归对线性分类关系的拟合效果好到丧心病狂

特征与标签之间的线性关系极强的数据&＃xff0c;比如金融领域中的信用卡欺诈&＃xff0c;评分卡制作&＃xff0c;电商中的营销预测等等相关的数据&＃xff0c;都是逻辑回归的强项。

虽然现在有了梯度提升树GDBT&＃xff0c;比逻辑回归效果更好&＃xff0c;也被许多数据咨询公司启用&＃xff0c;但逻辑回归在金融领域&＃xff0c;尤其是银行业中的统治地位依然不可动摇&＃xff08;相对的&＃xff0c;逻辑回归在非线性数据的效果很多时候比瞎猜还不如&＃xff0c;所以如果你已经知道数据之间的联系是非线性的&＃xff0c;千万不要迷信逻辑回归&＃xff09;

&＃xff08;2&＃xff09;逻辑回归计算快&＃xff1a;

对于线性数据&＃xff0c;逻辑回归的拟合和计算都非常快&＃xff0c;计算效率优于SVM和随机森林&＃xff0c;亲测表示在大型数据上尤其能够看得出区别。

&＃xff08;3&＃xff09;逻辑回归返回的分类结果不是固定的0&＃xff0c;1&＃xff0c;而是以小数形式呈现的类概率数字

在有些分类中&＃xff0c;返回的结果是0或1的数值&＃xff0c;没有中介结果。而逻辑回归输出的是[0,1]的小数

我们因此可以把逻辑回归返回的结果当成连续型数据来利用。比如在评分卡制作时&＃xff0c;我们不仅需要判断客户是否会违约&＃xff0c;还需要给出确定的”信用分“&＃xff0c;而这个信用分的计算就需要使用类概率计算出的对数几率&＃xff0c;而决策树和随机森林这样的分类器&＃xff0c;可以产出分类结果&＃xff0c;却无法帮助我们计算分数&＃xff08;当然&＃xff0c;在sklearn中&＃xff0c;决策树也可以产生概率&＃xff0c;使用接口predict_proba调用就好&＃xff0c;但一般来说&＃xff0c;正常的决策树没有这个功能&＃xff09;。

即我们不仅仅需要知道信用的等级或好坏&＃xff0c;我们还需要知道好的什么程度&＃xff0c;坏到什么程度。如10%&＃xff0c; 20%&＃xff0c;30%&＃xff0c; 40%&＃xff0c;50%&＃xff0c;60%&＃xff0c;70%&＃xff0c;80%&＃xff0c;90%&＃xff0c;100%&＃xff0c;如果是而分类&＃xff0c;只有0和1&＃xff0c;分界点可能是50%。

&＃xff08;4&＃xff09;逻辑回归的灵活性

然而&＃xff0c;60%和90%都归为1&＃xff0c;但他们程度是不同的。我们还需要对他们进行进一步的划分&＃xff0c;如划分为等级A, B, C, D.....等等&＃xff0c;这就给逻辑回归的输出 结果的使用带来了极大灵活性&＃xff0c;我们可以利用输出&＃xff0c;完成二分类&＃xff0c;也可以用输出结果大多多分类的效果。

&＃xff08;5&＃xff09;另外&＃xff0c;逻辑回归还有抗噪能力强的优点。

福布斯杂志在讨论逻辑回归的优点时&＃xff0c;甚至有着“技术上来说&＃xff0c;最佳模型的AUC面积低于0.8时&＃xff0c;逻辑回归非常明显优于树模型”的说法。并且&＃xff0c;逻辑回归在小数据集上表现更好&＃xff0c;在大型的数据集上&＃xff0c;树模型有着更好的表现。由此&＃xff0c;我们已经了解了逻辑回归的本质&＃xff0c;它是一个返回对数几率的&＃xff0c;在线性数据上表现优异的分类器&＃xff0c;它主要被应用在金融领域。其数学目的是求解能够让模型对数据拟合程度最高的参数 的值&＃xff0c;以此构建预测函数 &＃xff0c;然后将特征矩阵输入预测函数来计算出逻辑回归的结果y。注意&＃xff0c;虽然我们熟悉的逻辑回归通常被用于处理二分类问题&＃xff0c;但逻辑回归也可以做多分类。

第8本章 逻辑回归分类

根据拟合函数的类型&＃xff0c;分为

8.1 线性回归

线性回归就利用多个线性直线函数叠加作为拟合函数。

8.2 非线性回归

&＃xff08;1&＃xff09;概述

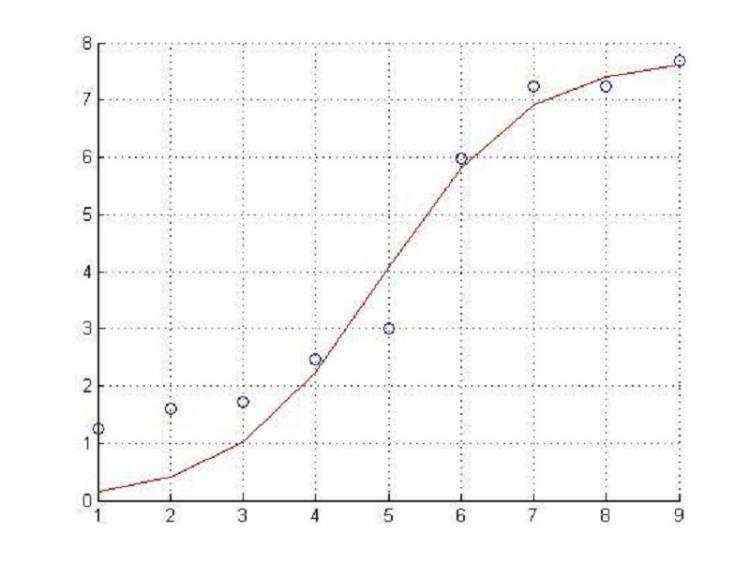
非线性回归就利用多个非线性函数的叠加作为拟合函数&＃xff1a;

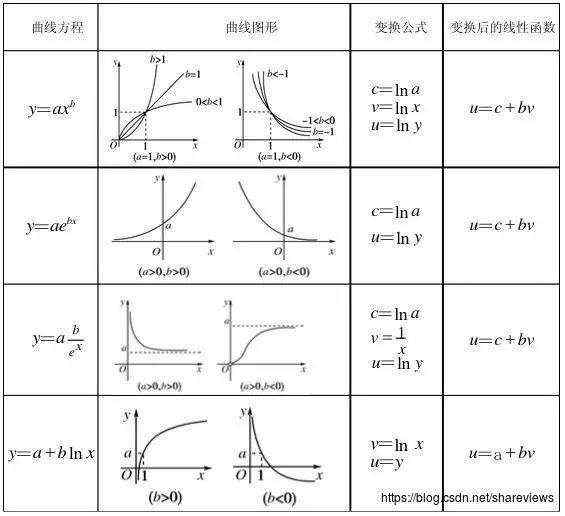
&＃xff08;2&＃xff09;常见的非线性函数就是多项式函数&＃xff1a;

多项式函数&＃xff0c;是数学概念。形如f(x)&＃61;an·x^n&＃43;an-1·x^(n-1)&＃43;…&＃43;a2·x^2&＃43;a1·x&＃43;a0的函数&＃xff0c;叫做多项式函数&＃xff0c;它是由常数与自变量x经过有限次乘法与加法运算得到的。显然&＃xff0c;当n&＃61;1时&＃xff0c;其为一次函数y&＃61;kx&＃43;b&＃xff0c;当n&＃61;2时&＃xff0c;其为二次函数。

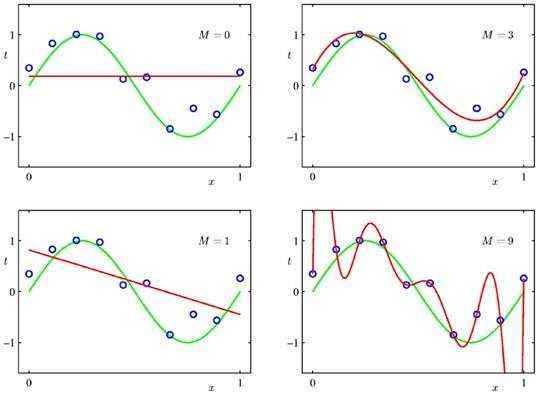
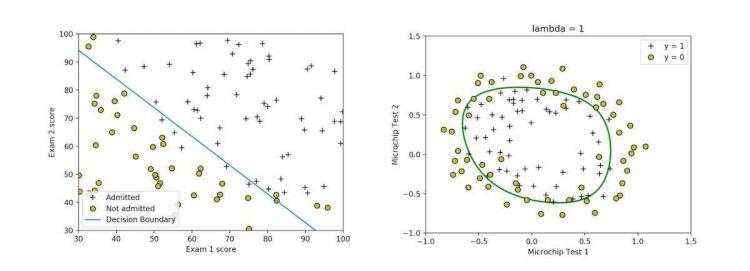
&＃xff08;3&＃xff09;多项式可以处理非常复杂的分类问题&＃xff1a;

作者主页(文火冰糖的硅基工坊)&＃xff1a;文火冰糖&＃xff08;王文兵&＃xff09;的博客_文火冰糖的硅基工坊_CSDN博客

本文网址&＃xff1a;